이산수학 논리파트 들어가겠습니다.
진릿값과 명제
명제는 객관적으로 참이나 거짓을 구별할 수 있어야 한다. 즉,멀다 가깝다 같은 주관적인 판단으로 답이 결정되는 문장은 명제가 될 수 없고,
있다, 없다, 1000개 이상이다 등과 같이 객관적으로 참, 거짓을 결정할 수 있는 문장은 명제가 될 수 있다.
진릿값은 참(T)이나 거짓(F)를 가리키는 값이다.
예를들어, 대한민국의 수도는 서울특별시이다. 는 참인 명제이다
아이폰15는 비싸다.는 명제가 될 수 없다. 왜냐하면 주관적인 판단이기 때문이다.
1+24=41452 는 거짓인 명제이다. 이유는 참,거짓을 판단할 수 있기 때문이다.
논리연산자
수학적 논리에서는 하나 이상의 명제를 결합하여 새로운 명제를 만들어낼 수도 있다.
명제들은 결합하기 위해서 부정,논리곱,논리합,베타적 논리합 과 같은 논리연산자(Logical Opreation)을 이용한다.
결합된 명제도 참, 거짓을 구분할 수 있는데 각 명제의 진릿값에 따른 논리연산의 결과를 보여주는 표를 진리표(Truth Table)라고 한다.
부정(NOT)
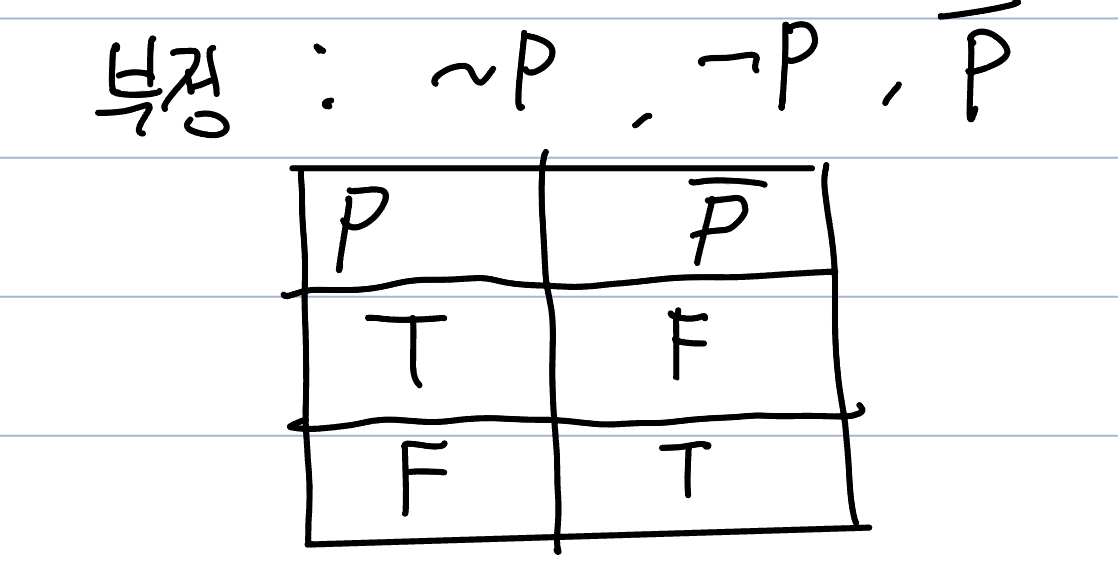
p가 아니다, not p, p의 부정 으로 읽을 수 있다. 표현 방법은 위에 3가지 방법이 있다. 진리표를 보면. 말 그대로 참이면 거짓, 거짓이면 참. 부정을 한 것이다.
논리곱(AND)

p and q로 읽을 수 있다. 표현 방법은 위에 3가지 방법이 있다. 진리표를 보면 동시에 참을 만족해야지 참이고 나머지 경우는 거짓이된다.
논리합(OR)

p or q로 읽을 수 있다. 표현방법은 위에 2가지 방법이 있다. 진리표를 보면 p q 둘중에 하나만 참이어도 참이고 둘다 거짓이어야지 거짓이 된다.
배타적 논리합(XOR)

p xor q로 읽을 수 있다. 진리표를 보면 서로 값이 달라야지 참이되고, 서로 값이 같으면 거짓이 된다.
합성명제,논리연산자의 우선순위
합성명제는 하나 이상의 명제들이 논리연산자에 의해 결합된 명제이다.
논리연산자의 우선순위는 이렇다.
1. ( )
2. NOT연산자
3. AND연산자
4.OR연산자
5. -> (조건명제)
6. <-> (쌍방조건명제)
항진명제,모순명제
항진명제 : 합성명제를 구성하는 단일명제의 진릿값에 상관없이 진릿값이 항상 참인 명제
모순명제 : 합성명제를 구성하는 단일명제의 진릿값에 상관없이 진릿값이 항상 거짓인 명제
사건명제
항진명제도 모순명제도 아닌 합성명제
조건명제 : p->q
문장 p, q가 명제일 때, 명제 p가 가정 또는 전제이고, 명제 q가 결론 또는 결과가 되는 명제
조건명제 p->q는 가정명제 p가 참이고, 결론 명제 q가 거짓이 되는 경우에만 거짓이된다. 그 외의 경우에는 참임.

p의 참이 비가오면 q의 참이 우산을 가지고 나간다 라고~ 생각해보자
위에서부터
비가 오면 우산을 가지고 나간다(이상하지 않음)
비가오면 우산을 가지고 나가지 않는다(이상함)
비가안오면 우산을 가지고 나간다(우산을 가지고 나갈수는 있기때문에 이상하지 않음)
비가안오면 우산을 가지고 나가지 않는다(이상하지 않음)
이렇게 생각하면 가정명제 p가 참(비가오면)일때 결론명제 q가 거짓(우산을 가지고 나가지 않음)만 이상하므로 이 경우에만 거짓이다.
쌍방조건명제 : p<->q
문장 p,q가 명제일 때, 명제 p와 q가 가정이면서 동시에 결론인 명제
조건명제에서는 가정명제p가 참이고 결론명제 q가 거짓일 때만 거짓이고 그 외의 경우에는 모두 참이었다.
그런데 쌍방조건명제는 명제 p,q 모두 가정이면서 결론이 될 수 있기 때문에 명제 p,q의 진릿값이 같을때만 참이되고, 그렇지 않을때는 거짓이 된다.
쌍방조건명제 진리표

역,이,대우
역,이,대우는 그림 하나도 표현 할 수 있다.

참…쉽죠…??? 이상으로 포스팅을 마치겠습니다요..
'학과 공부 > 이산수학' 카테고리의 다른 글
| 변수를 포함하는 명제, 추론[이산수학] (0) | 2023.10.09 |
|---|---|
| 논리적 동치[이산수학] (2) | 2023.10.09 |
| 컴퓨터에서의 수의 표현,보수의 10진수 변환, 보수의 연산[이산수학] (0) | 2023.10.07 |
| 1의보수, 2의보수[이산수학] (1) | 2023.10.07 |
| 수의 표현,bit,byte,word[이산수학] (1) | 2023.10.07 |
이산수학 논리파트 들어가겠습니다.
진릿값과 명제
명제는 객관적으로 참이나 거짓을 구별할 수 있어야 한다. 즉,멀다 가깝다 같은 주관적인 판단으로 답이 결정되는 문장은 명제가 될 수 없고,
있다, 없다, 1000개 이상이다 등과 같이 객관적으로 참, 거짓을 결정할 수 있는 문장은 명제가 될 수 있다.
진릿값은 참(T)이나 거짓(F)를 가리키는 값이다.
예를들어, 대한민국의 수도는 서울특별시이다. 는 참인 명제이다
아이폰15는 비싸다.는 명제가 될 수 없다. 왜냐하면 주관적인 판단이기 때문이다.
1+24=41452 는 거짓인 명제이다. 이유는 참,거짓을 판단할 수 있기 때문이다.
논리연산자
수학적 논리에서는 하나 이상의 명제를 결합하여 새로운 명제를 만들어낼 수도 있다.
명제들은 결합하기 위해서 부정,논리곱,논리합,베타적 논리합 과 같은 논리연산자(Logical Opreation)을 이용한다.
결합된 명제도 참, 거짓을 구분할 수 있는데 각 명제의 진릿값에 따른 논리연산의 결과를 보여주는 표를 진리표(Truth Table)라고 한다.
부정(NOT)

p가 아니다, not p, p의 부정 으로 읽을 수 있다. 표현 방법은 위에 3가지 방법이 있다. 진리표를 보면. 말 그대로 참이면 거짓, 거짓이면 참. 부정을 한 것이다.
논리곱(AND)

p and q로 읽을 수 있다. 표현 방법은 위에 3가지 방법이 있다. 진리표를 보면 동시에 참을 만족해야지 참이고 나머지 경우는 거짓이된다.
논리합(OR)

p or q로 읽을 수 있다. 표현방법은 위에 2가지 방법이 있다. 진리표를 보면 p q 둘중에 하나만 참이어도 참이고 둘다 거짓이어야지 거짓이 된다.
배타적 논리합(XOR)

p xor q로 읽을 수 있다. 진리표를 보면 서로 값이 달라야지 참이되고, 서로 값이 같으면 거짓이 된다.
합성명제,논리연산자의 우선순위
합성명제는 하나 이상의 명제들이 논리연산자에 의해 결합된 명제이다.
논리연산자의 우선순위는 이렇다.
1. ( )
2. NOT연산자
3. AND연산자
4.OR연산자
5. -> (조건명제)
6. <-> (쌍방조건명제)
항진명제,모순명제
항진명제 : 합성명제를 구성하는 단일명제의 진릿값에 상관없이 진릿값이 항상 참인 명제
모순명제 : 합성명제를 구성하는 단일명제의 진릿값에 상관없이 진릿값이 항상 거짓인 명제
사건명제
항진명제도 모순명제도 아닌 합성명제
조건명제 : p->q
문장 p, q가 명제일 때, 명제 p가 가정 또는 전제이고, 명제 q가 결론 또는 결과가 되는 명제
조건명제 p->q는 가정명제 p가 참이고, 결론 명제 q가 거짓이 되는 경우에만 거짓이된다. 그 외의 경우에는 참임.

p의 참이 비가오면 q의 참이 우산을 가지고 나간다 라고~ 생각해보자
위에서부터
비가 오면 우산을 가지고 나간다(이상하지 않음)
비가오면 우산을 가지고 나가지 않는다(이상함)
비가안오면 우산을 가지고 나간다(우산을 가지고 나갈수는 있기때문에 이상하지 않음)
비가안오면 우산을 가지고 나가지 않는다(이상하지 않음)
이렇게 생각하면 가정명제 p가 참(비가오면)일때 결론명제 q가 거짓(우산을 가지고 나가지 않음)만 이상하므로 이 경우에만 거짓이다.
쌍방조건명제 : p<->q
문장 p,q가 명제일 때, 명제 p와 q가 가정이면서 동시에 결론인 명제
조건명제에서는 가정명제p가 참이고 결론명제 q가 거짓일 때만 거짓이고 그 외의 경우에는 모두 참이었다.
그런데 쌍방조건명제는 명제 p,q 모두 가정이면서 결론이 될 수 있기 때문에 명제 p,q의 진릿값이 같을때만 참이되고, 그렇지 않을때는 거짓이 된다.
쌍방조건명제 진리표

역,이,대우
역,이,대우는 그림 하나도 표현 할 수 있다.

참…쉽죠…??? 이상으로 포스팅을 마치겠습니다요..
'학과 공부 > 이산수학' 카테고리의 다른 글
| 변수를 포함하는 명제, 추론[이산수학] (0) | 2023.10.09 |
|---|---|
| 논리적 동치[이산수학] (2) | 2023.10.09 |
| 컴퓨터에서의 수의 표현,보수의 10진수 변환, 보수의 연산[이산수학] (0) | 2023.10.07 |
| 1의보수, 2의보수[이산수학] (1) | 2023.10.07 |
| 수의 표현,bit,byte,word[이산수학] (1) | 2023.10.07 |
