오늘은 이산수학 중 관계(Relation)에 대해서 할 것이다.
먼저 기본용어인 정의역,공변역,치역,역관계에대해서 알아보고 그 후 관계의 표현 방법에 대해서 알아볼 것이다.
1. 정의역(Domain : dom(R))

2. 공변역 (Coomain : codom(R))

3. 치역(Range : ran(R))
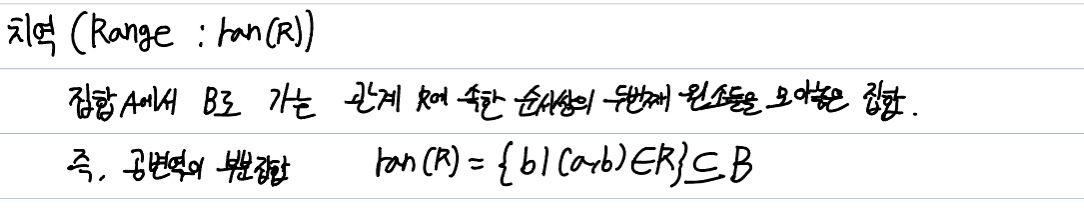
4.역관계(Inverse Relation : R^-1)

아마 이렇게 글로만 봤을 때는 이해가 안될것이다. 근데 예제를 풀면 아주 쉽게 이해할 수 있다.

문제를 풀어보자면,
정의역=dom(R)=A={a,b,c,d}
공변역=codom(R)=B={p,q,r}
치역=ran(R)={p,r}
이다. 치역은 두번째 원소에서 R에 포함되지 않은 원소는 빼주면 된다.
이제 이러한 관계들을 표현하는 방법들을 알아보겠다.
총 4가지 방법을 소개 할 것인데
1.화살표 선도 2.좌표도표 3.방향그래프 4.관계행렬이다.
1.화살표선도

2.좌표도표

3.방향그래프

4.관계행렬

위에서 말했듯이, 관계행렬 R의 역관계는 행렬 R과의 전치행렬 관계가 있다.
나는 관계행렬이 가장 편하므로 아래서부터는 관계행렬로 설명할 것이다.
이러한 관계들에도 반사관계,비반사관계,대칭관계,반대칭관계 가 있다.
순서대로 한번 알아보도록 하겠다.
1.반사관계

즉, 관계행렬로 나타냈을 때 , 대각원소들이 모두 1이면 반사관계이다.
2.비반사관계

비반사관계는 대각원소들이 모두 0이여야 한다. 하나라도 1이면 비반사관계가 아니다.
예를 보자면,

이런 관계행렬이 있다고 했을 때, 이 관계행렬은 대각원소가 모두 1도, 모두 0도 아니므로 반사관계,비반사관계 모두 아니다.
3.대칭관계

대각선을 중심으로 대칭인 원소가 1로 ’모두‘ 같으면 대칭관계이다.
원소가 0일경우 신경쓰지 않아도 된다.
4.반대칭관계

대각선을 중심으로 대칭인 원소가 모두 같지 않으면 반대칭관계이다.

그렇다면 이 관계행렬은 대칭관계일까 반대칭관계일까?
정답은 대각원소 외에 원소에 1이 없으므로 대칭과 반대칭 모두 된다.
대칭과 반대칭은 모두 될수도있고, 모두 안될수도 있다.
5.추이관계

말로하면 어렵지만 a가b로 가고 b가 c로 가면 a도 c로 가는 관계라는 소리이다.

이렇게 구할수 있다. 2 -> 3 을 보면 3으로 시작하는 원소가 없으므로 추이관계이다. 따라서 위에 관계는 추이관계를 성립한다.
예제를 하나 더 보자면

(a,b)가 없으므로 추이관계가 성립하지 않는다.
+문제풀이

이상입니다.
'학과 공부 > 이산수학' 카테고리의 다른 글
| 함수[이산수학] (1) | 2023.11.09 |
|---|---|
| 관계(2)[이산수학] (0) | 2023.10.31 |
| 변수를 포함하는 명제, 추론[이산수학] (0) | 2023.10.09 |
| 논리적 동치[이산수학] (2) | 2023.10.09 |
| 명제, 논리연산자, 역,이,대우 [이산수학] (1) | 2023.10.07 |
