이번 글에서는 함수에 대해서 알아 볼 것이다. 목차는 함수의 개념, 함수의 종류, 합성함수, 함수의 특성에 대해서이다.
함수의 개념
함수(Function : A->B)
집합 A,B에 대해 집합 A에서 B로 가는 관계가 성립할 때, 집합 A의 원소 a에 대해 집합 B의 원소 b 하나가 대응되는 관계
즉, 하나의 입력값에서 하나의 출력값이 나와야한다. 그림으로 보자면

이렇게 f(a)=1, f(a)=2가 나오면 안된다. 오직 하나의 출력값만이 나와야한다.
단사함수(injective function)

쉽게 말하자면, 정의역의 원소들이 공변역의 원소들이랑 한놈씩 대응하는 함수이다.

이런 함수가 단사함수이다.

이것도 단사함수이다. 근데 공변역에 원소가 더 많으면 인기없는 원소들은 정의역한테 선택을 못받을 수도 있음…
전사함수(Subject Function)

이걸 간단히 말로 풀어보면, 그냥 공변역의 모든 원소들이 화살표로 선택을 받아야하는 함수이다. 근데 공변역의 원소들은 양다리가 가능하다(;;;;;) 그것이 전사함수… 응…

이렇게 공변역의 모든 원소가 선택을 받아야한다.

전단사함수
말 그대로 단사함수이면서 전사함수인 함수이다. 그럴려면 정의역과 공변역의 원소의 갯수가 같아야한다. 예시를 보자면

이렇게 각각 하나씩 모두 대응해야한다.
역함수

역함수는 전단사함수 일 경우에만 존재한다. 예시를 보자면

우선 함수가 역함수를 가질 수 있는 가역함수인지 확인해야한다. 즉, 전단사 함수인지 확인을 한 후, 역함수를 구해주면 된다.
합성함수(Composition Function)

합성함수도 관계와 마찬가지로 뒤에있는 걸 먼저 앞에있는걸 나중에 해준다.
이걸 그림으로 간단히 나타내면
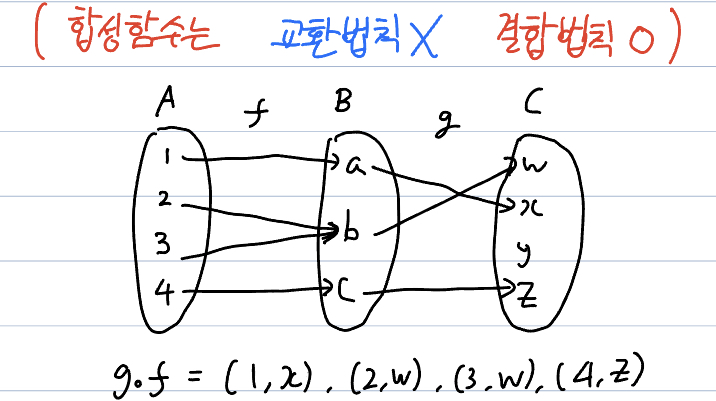
이렇게 나타낼 수 있다. 합성함수는 결합법칙은 가능하지만 교환법칙은 안된다.
항등함수(Identitiy Function)

이거는 쉽게 풀어써져있다. f(a) = a 인 함수이다. 그리고 항등함수와 다른 함수를 합성하면 그 결과는 다른 함수값이 나온다.

이렇게…
상수함수(Constant Function)

모든 입려겡 대해 출력이 하나인 함수이다. 즉 f(a)도 1, f(b)도 1 f(c)도 1의 결과값이 나오는 함수를 상수함수라고 한다.
특성함수(Characteristic Function)
결과값이 0,1 밖에 없는 함수를 특성함수라고 한다.
바닥함수(Floor Function)

말 그대로 x보다는 작지만 그 중에서는 짱인 정수이다. 마치…뱀의 머리같은 함수.. 입시로 따지면 하향인데 장학금받고 학교다니는거
천정함수(Ceiling Function)

이건 반대로 x보다는 크지만 그 중에서는 가장 쩌리인 정수이다. 용의 꼬리인 함수라고도 할수도 있겠따…. 커트라인 딱 되서 문닫고 입시성공한 거임….
함수는 이정도까지만.. 개념만 알고 넘어가겠습니다..
'학과 공부 > 이산수학' 카테고리의 다른 글
| 트리[이산수학] (4) | 2023.11.22 |
|---|---|
| 그래프[이산수학] (2) | 2023.11.22 |
| 관계(2)[이산수학] (0) | 2023.10.31 |
| 관계[이산수학] (1) | 2023.10.30 |
| 변수를 포함하는 명제, 추론[이산수학] (0) | 2023.10.09 |
