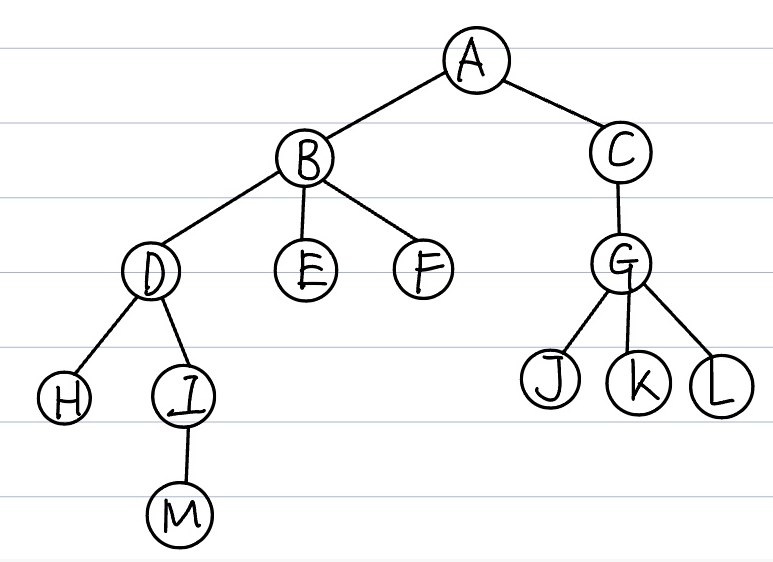
트리(Tree)
루트라는 특별한 노드를 갖고 그래프를 구성하는 단순경로가 존재하는 비순환의 연결그래프
노드(Node)
트리인 그래프 T를 구성하는 꼭짓점
루트(Root)
트리인 그래프 T의 가장 높은 곳에 위치하는 시작노트
->A
부모 노드(Parent Node)
임의의 노드의 한 단계 상위 노드
자식 노드(Child Node)
임의의 노드의 한 단계 하위 노드
형제 노드(Sibling Node)
임의의 노드와 부모가 같은 노드
리프 노드(Leaf Node)
자식 노드가 없는 노드
중간 노드(Internal Node)
루트 노드나 리프 노드가 아닌 노드
조상 노드(Ancestor Node)
임의의 한 노드에 이르는 경로에 포함된 모든 노드들
자손 노드(Descendant Node)
임의의 한 노드에서 리프 노드에 이르는 경로에 포함된 모든 노드들
서브 트리(Sub Tree)
임의의 한 노드를 루트로 하는 트리
차수(Degree)
트리인 그래프 T의 임의의 한 노드에 포함된 자식 노드의 개수
레벨(Level)
트리인 그래프 T의 루트 노드를 레벨 0으로 시작하여 자식 노드로 한 단계씩 내려갈 때마다 하나 씩 증가하는 단계
높이(Height)
트리인 그래프 T의 최대 레벨
이진트리(Binary Tree)
차수가 최대 2인 트리(1도 가능)
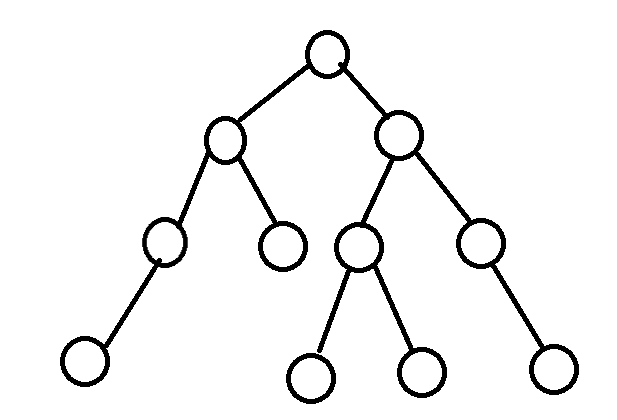
완전 이진 트리(Complete Binary Tree)
높이가 h일때 레벨 1부터 h-2까지의 모든 노드의 차수가 2이고, 레벨 h는 왼쪽부터 노드가 채워져 있는 트리
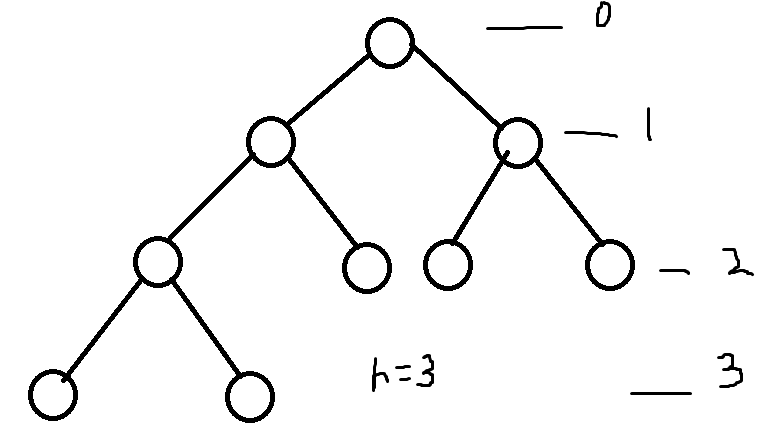
높이가 3이므로 h-2는 1이다.따라서 1레벨 노드의 차수가 모두 2여야 한다. 또한 레벨 3은 왼쪽부터 노드가 채워져 있으므로완전 이진 트리이다.
포화이진트리(Full Binary Tree)
높이가 h일때 레벨 0부터 h-1까지의 모든 노드의 차수가 2인 트리
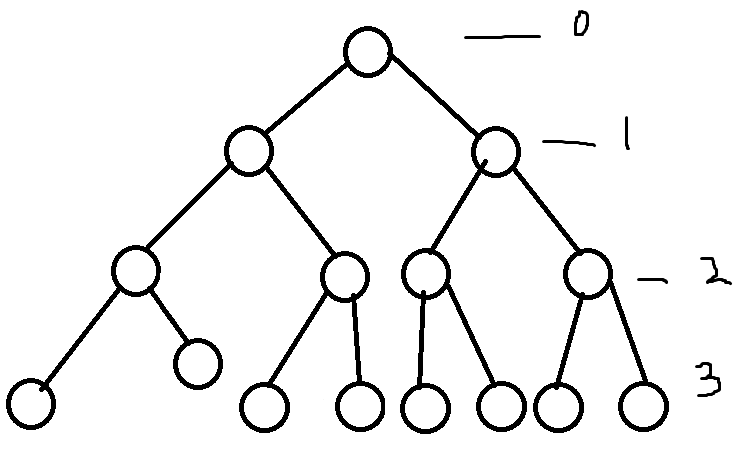
편향 이진 트리(Skewed Binary Tree)
왼쪽이나 오른쪽 서브 트리만 가지는 트리
이진트리의 노드 수 정리
1. 레벨 k에서 가질 수 있는 최대 노드 수 : 2^k 개 -> // ex)레벨 3이면 8개, 레벨 10이면 1024개
2. 높이가 m인 이진 트리가 가질 수 있는 최대 노드 수 : 2^(m+1)-1개 ->//ex) 높이가 3이면 16-1=15개(포화 이진 트리)
3. 높이가 m인 이진 트리가 가질 수 있는 최소 노드 수 : m+1개 ->//ex)높이가 3이면 최소 노드 수는 4개(편향 이진 트리)
이진트리의 순회
모든 노드의 데이터를 처리할 수 있도록 한번씩 방문하는 방법을 순회라고 한다. 전위,중위,후위 순회가 있다.
1.전위순회
부모노드-> 왼쪽 자식노드-> 오른쪽 자식노드 순으로 탐색하는 순회방식(부왼오)
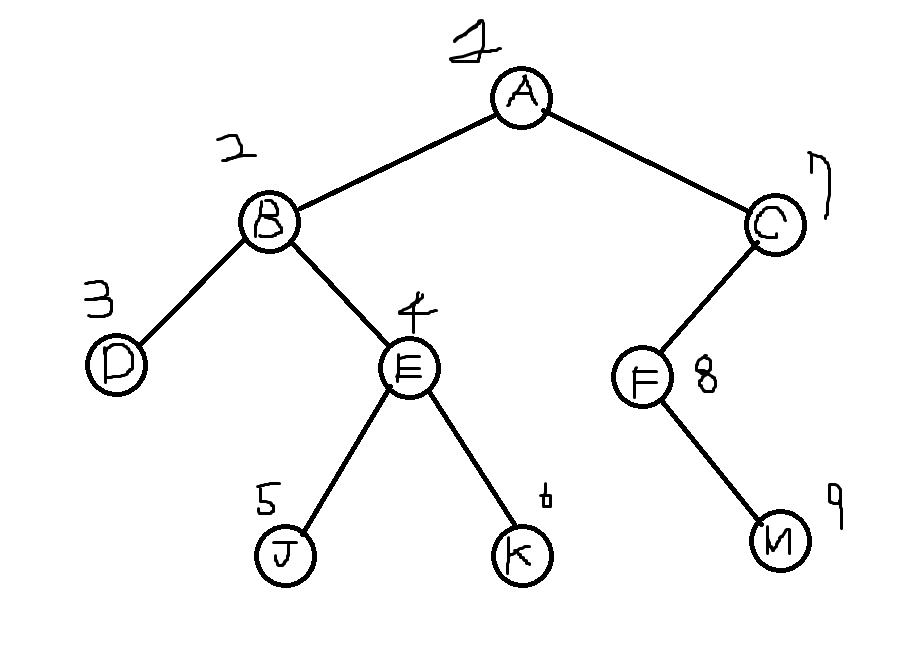
2. 중위순회
왼쪽 자식노드-> 부모노드-> 오른쪽 자식노드 순으로 탐색하는 순회방식(왼부오)

3. 후위순회
왼쪽 자식노드-> 오른쪽 자식노드-> 부모노드 순으로 탐색하는 순회방식(왼오부)
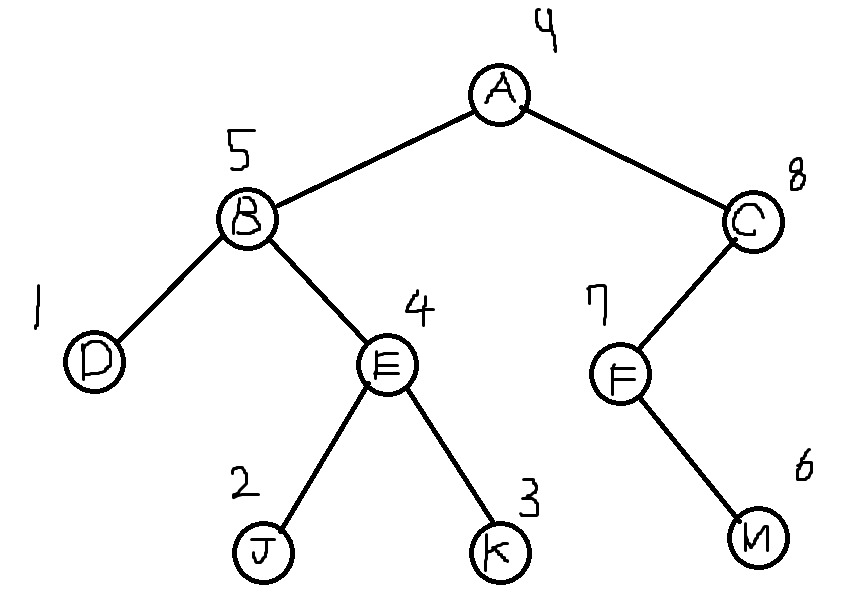
이런식으로 각각 다른 방식으로 탐색할 수 있다.
이진 탐색 트리(Binary Search Tree)
노드가 가지는 데이터의 내용에 대한 기준에 다라 노드의 위치를 탐색할 수 있는 트리

이렇게 부모노드보다 작으면 왼쪽으로 크면 오른쪽으로 정렬되어있는 트리를 이진 탐색 트리라고 한다.
'학과 공부 > 이산수학' 카테고리의 다른 글
| 프림 알고리즘,크루스칼 알고리즘,허프만 알고리즘[이산수학] (1) | 2023.11.23 |
|---|---|
| 그래프[이산수학] (2) | 2023.11.22 |
| 함수[이산수학] (1) | 2023.11.09 |
| 관계(2)[이산수학] (0) | 2023.10.31 |
| 관계[이산수학] (1) | 2023.10.30 |

트리(Tree)
루트라는 특별한 노드를 갖고 그래프를 구성하는 단순경로가 존재하는 비순환의 연결그래프
노드(Node)
트리인 그래프 T를 구성하는 꼭짓점
루트(Root)
트리인 그래프 T의 가장 높은 곳에 위치하는 시작노트
->A
부모 노드(Parent Node)
임의의 노드의 한 단계 상위 노드
자식 노드(Child Node)
임의의 노드의 한 단계 하위 노드
형제 노드(Sibling Node)
임의의 노드와 부모가 같은 노드
리프 노드(Leaf Node)
자식 노드가 없는 노드
중간 노드(Internal Node)
루트 노드나 리프 노드가 아닌 노드
조상 노드(Ancestor Node)
임의의 한 노드에 이르는 경로에 포함된 모든 노드들
자손 노드(Descendant Node)
임의의 한 노드에서 리프 노드에 이르는 경로에 포함된 모든 노드들
서브 트리(Sub Tree)
임의의 한 노드를 루트로 하는 트리
차수(Degree)
트리인 그래프 T의 임의의 한 노드에 포함된 자식 노드의 개수
레벨(Level)
트리인 그래프 T의 루트 노드를 레벨 0으로 시작하여 자식 노드로 한 단계씩 내려갈 때마다 하나 씩 증가하는 단계
높이(Height)
트리인 그래프 T의 최대 레벨
이진트리(Binary Tree)
차수가 최대 2인 트리(1도 가능)

완전 이진 트리(Complete Binary Tree)
높이가 h일때 레벨 1부터 h-2까지의 모든 노드의 차수가 2이고, 레벨 h는 왼쪽부터 노드가 채워져 있는 트리

높이가 3이므로 h-2는 1이다.따라서 1레벨 노드의 차수가 모두 2여야 한다. 또한 레벨 3은 왼쪽부터 노드가 채워져 있으므로완전 이진 트리이다.
포화이진트리(Full Binary Tree)
높이가 h일때 레벨 0부터 h-1까지의 모든 노드의 차수가 2인 트리

편향 이진 트리(Skewed Binary Tree)
왼쪽이나 오른쪽 서브 트리만 가지는 트리

이진트리의 노드 수 정리
1. 레벨 k에서 가질 수 있는 최대 노드 수 : 2^k 개 -> // ex)레벨 3이면 8개, 레벨 10이면 1024개
2. 높이가 m인 이진 트리가 가질 수 있는 최대 노드 수 : 2^(m+1)-1개 ->//ex) 높이가 3이면 16-1=15개(포화 이진 트리)
3. 높이가 m인 이진 트리가 가질 수 있는 최소 노드 수 : m+1개 ->//ex)높이가 3이면 최소 노드 수는 4개(편향 이진 트리)
이진트리의 순회
모든 노드의 데이터를 처리할 수 있도록 한번씩 방문하는 방법을 순회라고 한다. 전위,중위,후위 순회가 있다.
1.전위순회
부모노드-> 왼쪽 자식노드-> 오른쪽 자식노드 순으로 탐색하는 순회방식(부왼오)

2. 중위순회
왼쪽 자식노드-> 부모노드-> 오른쪽 자식노드 순으로 탐색하는 순회방식(왼부오)

3. 후위순회
왼쪽 자식노드-> 오른쪽 자식노드-> 부모노드 순으로 탐색하는 순회방식(왼오부)

이런식으로 각각 다른 방식으로 탐색할 수 있다.
이진 탐색 트리(Binary Search Tree)
노드가 가지는 데이터의 내용에 대한 기준에 다라 노드의 위치를 탐색할 수 있는 트리

이렇게 부모노드보다 작으면 왼쪽으로 크면 오른쪽으로 정렬되어있는 트리를 이진 탐색 트리라고 한다.
'학과 공부 > 이산수학' 카테고리의 다른 글
| 프림 알고리즘,크루스칼 알고리즘,허프만 알고리즘[이산수학] (1) | 2023.11.23 |
|---|---|
| 그래프[이산수학] (2) | 2023.11.22 |
| 함수[이산수학] (1) | 2023.11.09 |
| 관계(2)[이산수학] (0) | 2023.10.31 |
| 관계[이산수학] (1) | 2023.10.30 |
