그래프의 차수(Degree)
꼭짓점 v에 근접하는 모서리의 수

이 그래프에서 꼭짓점 1의 차수는 1, 2의 차수는 3이다.
차수에대한 정리
1. 그래프G=(V,E)에서 모든 꼭짓점의 차수의 합은 모서리의 수의 두배이다.
위 그래프도 모서리의 수는 2이고 꼭짓점의 차수의 합은 4이다.
2. 그래프 G=(V,E) 에서 차수가 홀수이면 꼭짓점의 수는 짝수이다.(아니면 그래프가 아님)
부분그래프와 부분신장 그래프
부분 그래프 : 어떤 그래프 G에 포함되는 일부 꼭짓점과 모서리로만 그린 그래프
부분신장 그래프 : 부분 그래프 중에서 그래프 G의 꼭짓점을 모두 포함하지만 모서리는 일부만 포함하는 그래프

차례대로 그래프 G, 부분그래프, 부분신장 그래프이다.
부분그래프는 그래프 G에 속해있으면 되고, 부분신장 그래프는 모든 꼭짓점을 포함하게 속해있어야한다.
평면그래프
->그래프 G를 평면에 그릴 때, 꼭짓점이 아닌곳에서는 어떤 모서리도 교차하지 않는 그래프.
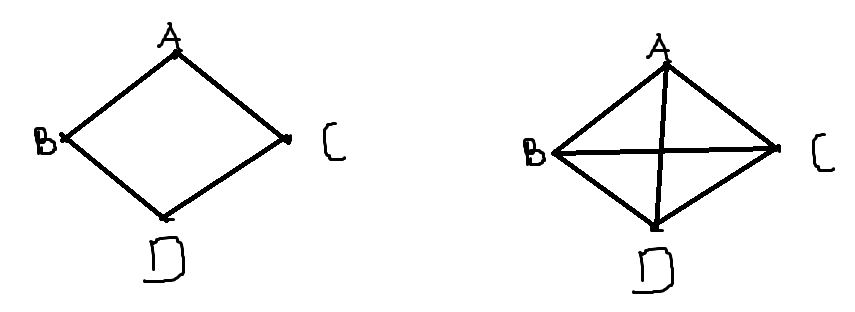
첫번째 그래프는 평면그래프이고 두번째 그래프는 평면그래프가 아니다.
오일러 공식
연결된 평면 그래프 G에서 꼭짓점의 수를 v, 모서리의 수를 e, 영역의 수를 s라고 할때
v-e+s = 2 인 오일러 공식이 성립한다.
위 첫번째 그래프를 보자면 v=4 e=4 s=2 이므로 4-4+2=2이므로 오일러공식이 성립한다.
연결그래프
그래프를 구성하는 모든 꼭짓점 사이에 경로가 존재하는 그래프
경로
그래프 G에 존재하는 임의의 꼭짓점 u,v 간의 길 중에서 같은 모서리를 두번 이상 포함하지 않는 길(왔다 갔다가 안됨)
완전그래프
n개의 꼭짓점 모두에 대해 근접하는 모서리의 수가 n-1개인 그래프
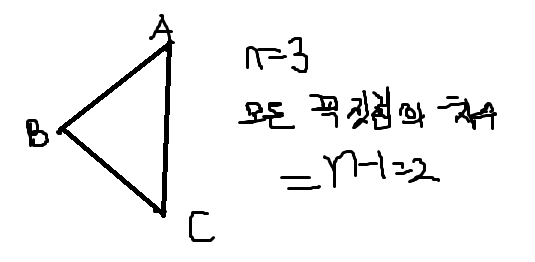
모든 꼭짓점의 차수가 2이므로 완전그래프라고 할 수 있다.
정규그래프
그래프 G내에 있는 모든 꼭짓점의 차수가 같은 그래프.
오일러와 해밀턴
순환 또는 회로
시작하는 꼭짓점과 끝나는 꼭짓점이 같은 경로
오일러 경로
그래프 G의 모든 변을 꼭 한번씩만 지나는 경로
오일러 순환
그래프 G의 꼭짓점 v에서 시작해 모든 변을 꼭 한번씩만 지나 다시 v로 돌아오는 경로
오일러 그래프
오일러 순환을 가지는 그래프 G //(한붓그리기 생각하면 됨)

오일러그래프에 대한 정리
1.연결 그래프 G의 모든 꼭짓점의 차수가 짝수이면, 오일러 그래프의 필요충분조건이 된다.
2. 연결 그래프 G의 꼭짓점 중 차수가 홀수인 꼭짓점의 수가 0또는 2개이면, 오일러 경로를 갖기위한 필요충분조건이다.
해밀턴경로
그래프 G의 모든 꼭짓점을 꼭 한번씩만 지나는 경로
해밀턴순환
그래프 G의 꼭짓점 v에서 시작해 모든 꼭짓점을 꼭 한번씩만 지나 다시 v로 돌아오는 경로
해밀턴 그래프
해밀턴 순환을 갖는 그래프 G

오일러 경로, 오일러 순환과는 다르게 해밀턴 경로, 해밀턴 순환은 같은 변을 몇번을 지나든 상관 X 오로지 꼭짓점들만 한번씩 지나면 됨.
'학과 공부 > 이산수학' 카테고리의 다른 글
| 프림 알고리즘,크루스칼 알고리즘,허프만 알고리즘[이산수학] (1) | 2023.11.23 |
|---|---|
| 트리[이산수학] (4) | 2023.11.22 |
| 함수[이산수학] (1) | 2023.11.09 |
| 관계(2)[이산수학] (0) | 2023.10.31 |
| 관계[이산수학] (1) | 2023.10.30 |
