신장트리(Spanning Tree)
그래프 G의 모든 꼭짓점을 노드로 포함하는 트리 T
최소신장트리(Minimal Spanning Tree)
그래프 G의 모든 꼭짓점을 노드로 포함하면서 노드 간의 비용을 최소로 하는 트리 T
최소신장트리를 유도하기 위해 프림 알고리즘이나 크루스칼 알고리즘을 활용함.
1.프림 알고리즘(Prim Algorithm)
(1)모든 변들 중 가중치가 가장 작은 변을 선택함.
(2)가중치가 작은쪽으로 변을 계속 이어나감
(3)순환이 형성되는 경우 그 변은 선택하지 않는다.
예제
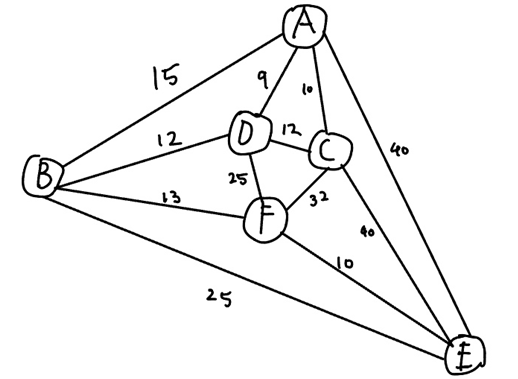
이런 그래프가 있다고 하면 프림 알고리즘의 순서는

이렇게 된다. 가중치가 작은 edge부터 이어가서 계속 작은 쪽으로 이어가면 결국 노드간의 비용이 가장 작아지는 트리가 나온다.
2.크루스칼 알고리즘(Kruskal Algorithm)
(1) 가중치가 가장 작은 모서리를 차례로 선택한다.
(2) 가중치가 같은 모서리는 모두 선택한다.
(3) 선택된 모서리에 의해 순환이 형성되는 경우는 선택하지 않는다.
(4) 그래프에 포함된 모든 꼭짓점의 수가 n개일 때, n-1개의 모서리가 연결되면 종료.

1번부터 가중치가 작은 A-D를 이어주고 순환되지 않게 트리 노드를 이어주면 된다.
3.허프만 알고리즘(Huffman Algorithm)
발생빈도가 높은 문자는 적은 비트를 할당하고 발생빈도가 낮은 문자에는 많은 비트를 할당하는 알고리즘
(1) 발생빈도가 가장 낮은 두 문자를 선택하여 하나의 이진 트리를 생성한다.
1.왼쪽 노드에 빈도수가 낮은 문자, 오른쪽 노드에 빈도 수가 높은 문자를 위치시킨다.
2.빈도수가 같은 경우는 사전적으로 앞에 오는 문자를 왼쪽에 위치시킨다.
3. 두 문자의 빈도의 합을 그 문자들의 부모 노드로 한다.
(2) (1)의 과정을 모든 문자가 하나의 이진트리로 묶일 때까지 반복한다.
(3) 생성된 이진 트리의 왼쪽노드에는 0, 오른쪽 노드에는 1을 부여한다.
(4) 루트부터 해당 문자까지의 0또는 1을 순서대로 나열한다.
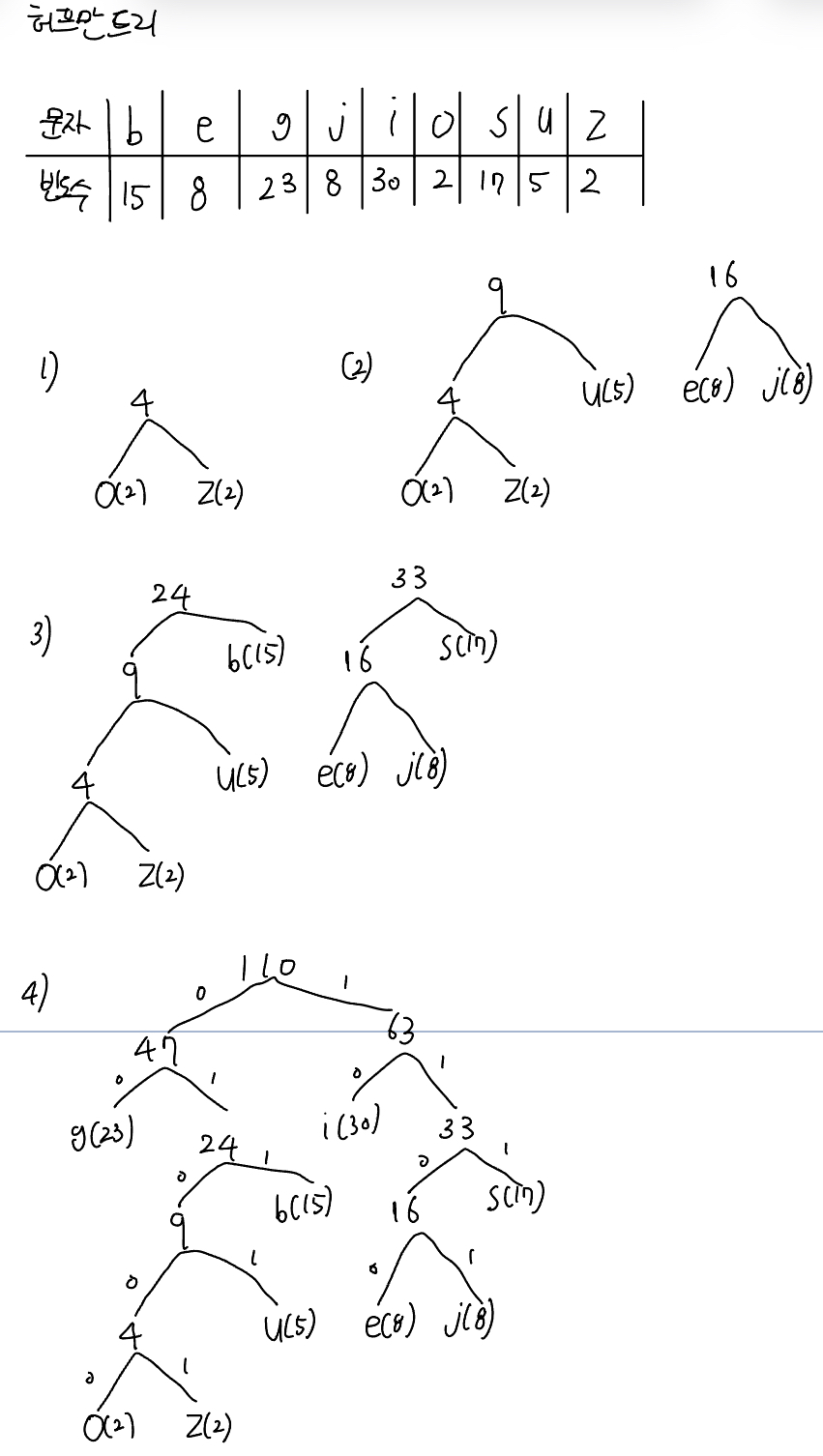
이렇게 허프만 트리를 작성할 수 있다.
각 문자를 코드로 나타내보면
g = 00
i = 10
b = 011
s = 111
u = 0101
e = 1100
j = 1101
o = 01000
z = 01001
이렇게 나타낼 수 있다. 이제 이 코드를 갖고 문자열을 코드로 변경할수도 있고, 코드를 문자열로 변경할수도 있다. 있어야한다
신장트리(Spanning Tree)
그래프 G의 모든 꼭짓점을 노드로 포함하는 트리 T
최소신장트리(Minimal Spanning Tree)
그래프 G의 모든 꼭짓점을 노드로 포함하면서 노드 간의 비용을 최소로 하는 트리 T
최소신장트리를 유도하기 위해 프림 알고리즘이나 크루스칼 알고리즘을 활용함.
1.프림 알고리즘(Prim Algorithm)
(1)모든 변들 중 가중치가 가장 작은 변을 선택함.
(2)가중치가 작은쪽으로 변을 계속 이어나감
(3)순환이 형성되는 경우 그 변은 선택하지 않는다.
예제

이런 그래프가 있다고 하면 프림 알고리즘의 순서는

이렇게 된다. 가중치가 작은 edge부터 이어가서 계속 작은 쪽으로 이어가면 결국 노드간의 비용이 가장 작아지는 트리가 나온다.
2.크루스칼 알고리즘(Kruskal Algorithm)
(1) 가중치가 가장 작은 모서리를 차례로 선택한다.
(2) 가중치가 같은 모서리는 모두 선택한다.
(3) 선택된 모서리에 의해 순환이 형성되는 경우는 선택하지 않는다.
(4) 그래프에 포함된 모든 꼭짓점의 수가 n개일 때, n-1개의 모서리가 연결되면 종료.

1번부터 가중치가 작은 A-D를 이어주고 순환되지 않게 트리 노드를 이어주면 된다.
3.허프만 알고리즘(Huffman Algorithm)
발생빈도가 높은 문자는 적은 비트를 할당하고 발생빈도가 낮은 문자에는 많은 비트를 할당하는 알고리즘
(1) 발생빈도가 가장 낮은 두 문자를 선택하여 하나의 이진 트리를 생성한다.
1.왼쪽 노드에 빈도수가 낮은 문자, 오른쪽 노드에 빈도 수가 높은 문자를 위치시킨다.
2.빈도수가 같은 경우는 사전적으로 앞에 오는 문자를 왼쪽에 위치시킨다.
3. 두 문자의 빈도의 합을 그 문자들의 부모 노드로 한다.
(2) (1)의 과정을 모든 문자가 하나의 이진트리로 묶일 때까지 반복한다.
(3) 생성된 이진 트리의 왼쪽노드에는 0, 오른쪽 노드에는 1을 부여한다.
(4) 루트부터 해당 문자까지의 0또는 1을 순서대로 나열한다.

이렇게 허프만 트리를 작성할 수 있다.
각 문자를 코드로 나타내보면
g = 00
i = 10
b = 011
s = 111
u = 0101
e = 1100
j = 1101
o = 01000
z = 01001
이렇게 나타낼 수 있다. 이제 이 코드를 갖고 문자열을 코드로 변경할수도 있고, 코드를 문자열로 변경할수도 있다. 있어야한다
